Resolving the St. Petersburg paradox
Originally proposed in 1713 by Nicolas Bernoulli, the St. Petersburg paradox is a famous economic and philosophical puzzle concerning a risky gamble on which people are invited to place a bet. The house offers to flip a coin until it comes up heads; the house pays $1 if heads appears on the first trial; otherwise the payoff doubles each time tails appears. This compounding stops and payment is given at the first heads. Despite the expected value of the St. Petersburg gamble being infinite, people are typically willing to place only a small bet on this gamble. This paradox elicited a variety of explanations from several notable thinkers, including Daniel and Nicolas Bernoulli, Cramer, de Morgan, Condorcet, Euler, Poisson, Gibbon, Marschack, Cournot, Arrow, Keynes, Stigler, Samuelson, von Mises, Ramsey, and Aumann. Nonetheless, there has been no widely accepted explanation of this paradox, and it has thus remained a mystery.
We show that the St. Petersburg paradox can be accounted for by a variant of normative expected utility valuation which acknowledges computational and cognitive limitations. Specifically, we demonstrate that our meta-cognitively rational model, sample-based expected utility (SbEU), can account for major experimental findings on the St. Petersburg paradox.
Our resolution of this paradox is consistent with two empirically well-supported assumptions: (a) people use only a few samples in probabilistic judgments and decision-making, and (b) people tend to overestimate the probability of extreme events in their judgment.
We show that the St. Petersburg paradox can be accounted for by a variant of normative expected utility valuation which acknowledges computational and cognitive limitations. Specifically, we demonstrate that our meta-cognitively rational model, sample-based expected utility (SbEU), can account for major experimental findings on the St. Petersburg paradox.
Our resolution of this paradox is consistent with two empirically well-supported assumptions: (a) people use only a few samples in probabilistic judgments and decision-making, and (b) people tend to overestimate the probability of extreme events in their judgment.
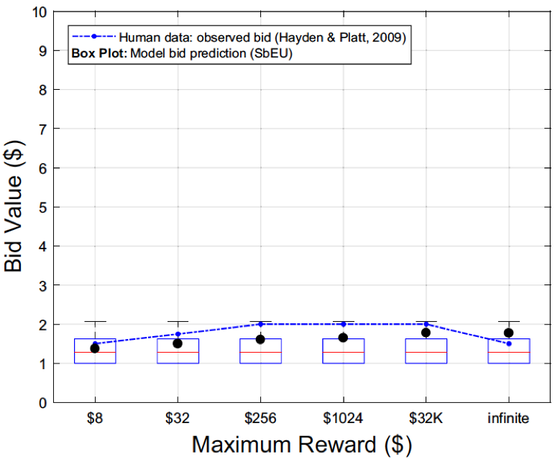
SbEU simulates the finding that peoples' bets are only weakly affect by game truncation.
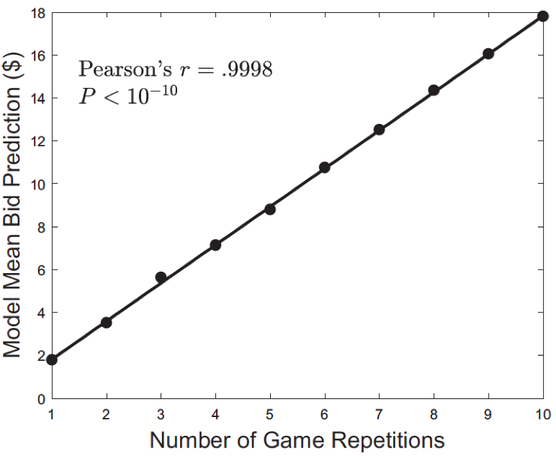
SbEU simulates peoples' tendency to place higher bets for more game repetitions.
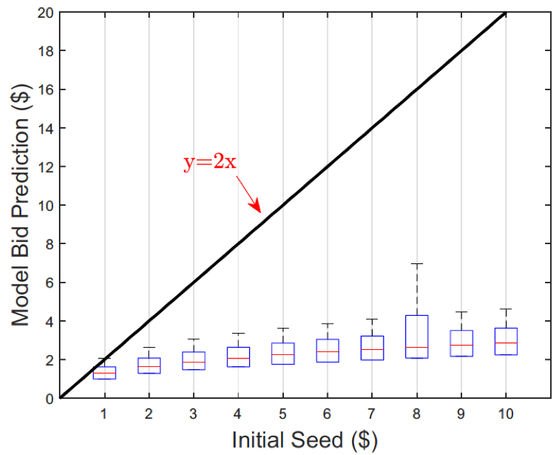
SbEU simulates the finding that people’s bets are typically lower than twice the smallest initial seed.
- Hayden, B. Y. & Platt, M. L. (2009). The mean, the median, and the St. Petersburg paradox. Judgment and decision making, 4(4), 256-272.
- Nobandegani, A. S. & Shultz, T. R. (2020). A resource-rational, process-level account of the St. Petersburg Paradox. Topics in Cognitive Science, 12, 417-432.